৮ম (অষ্টম) শ্রেণীর গণিত সমাধান অধ্যায়-৬ অবস্থান মানচিত্রে স্থানাংকে জ্যামিতি ২০২৪। Class 8 Math solution pdf 2024। ৮ম (অষ্টম) শ্রেণির গণিত বই সমাধান pdf

৮ম (অষ্টম) শ্রেণীর গণিত সমাধান অধ্যায়-৬ অবস্থান মানচিত্রে স্থানাংকে জ্যামিতি ২০২৪। Class 8 Math solution pdf 2024

৮ম (অষ্টম) শ্রেণীর গণিত সমাধান অধ্যায়-২ অবস্থান মানচিত্রে স্থানাংকে জ্যামিতি ২০২৪

প্রিয় শিক্ষার্থী, অষ্টম শ্রেণির নতুন শিক্ষাক্রমের সবাইকে স্বাগত। তোমরা নিশ্চয়ই জানো, জাতীয় শিক্ষাক্রম ও পাঠ্যপুস্তক বোর্ড অন্যান্য বইয়ের সাথে ২০২৪ শিক্ষাবর্ষে অষ্টম শ্রেণির জন্য নতুন গণিত পাঠ্যপুস্তকটিও অনুমোদন করেছে। গণিত পাঠ্যপুস্তকটি তৈরির সময় দুটি বিষয়ে সবচেয়ে বেশি গুরুত্ব দেওয়া হয়েছে। যথা—

১. চারপাশের পরিচিত পরিবেশের বস্তু ও ঘটনা পর্যবেক্ষণ করে হাতে–কলমে কাজের মাধ্যমে গাণিতিক সমস্যার সমাধান এবং

২. দৈনন্দিন জীবনে বিভিন্ন কাজে গাণিতিক দক্ষতা ব্যবহার করতে পারার সুযোগ সৃষ্টি করা।

প্রিয় শিক্ষার্থী, আমরা এখানে অষ্টম শ্রেণির নতুন বই ২০২৪ এর অনুসারে অধ্যায় ভিত্তিক সমাধান দেয়া হলো। কোন কিছু বাদ গেলে বা জানা থাকলে আমাদের সাথে যোগাযোগ করার অনুরোধ রইল। এখানে ধারাবাহিকভাবে গণিত বই এর সকল অধ্যায় এর সমাধান দেওয়া হবে।

৮ম(অষ্টম) শ্রেণীর গণিত সমাধান pdf ২০২৪। ৮ম(অষ্টম) শ্রেণির গণিত বই সমাধান ২০২৪

আজকের এই পোস্টের মাধ্যমে প্রিয় শিক্ষার্থীরা তোমরা পেয়ে যাবে অষ্টম শ্রেণীর গণিত সমাধান। ২০২৪ শিক্ষাবর্ষে অষ্টম শ্রেণীর গণিত বই এর নতুন সংস্করণ প্রকাশ করেছে শিক্ষাবোর্ড। ফলে অষ্টম শ্রেণির গণিত বই সমাধান এর গাইড বাজারেও এখনো বের হয়নি। ওয়েবসাইটেও সেভাবে পাওয়া যাচ্ছে না। কিন্তু শিক্ষার্থীদের সুবিধার কথা চিন্তা করে আমরা অষ্টম শ্রেণীর গণিত বই এর সমাধান নিয়ে এসেছি। আশাকরি এই সমাধান পেয়ে শিক্ষার্থীরা কিছুটা হলেও উপকৃত হবে। শিক্ষার্থীরা সামান্যতম উপকৃত হলে আমাদের শ্রম সার্থক বলে মনে করব। আমরা ধারাবাহিকভাবে প্রতিটি অধ্যায়ের এর সমাধান দেয়ার চেষ্টা করবো ইনশা আল্লাহ।

৮ম(অষ্টম) শ্রেণীর গণিত সমাধান pdf ২০২৪। Class 8 Math solution pdf 2024।

৮ম (অষ্টম) শ্রেণীর গণিত সমাধান অধ্যায়-৬ অবস্থান মানচিত্রে স্থানাংকে জ্যামিতি ২০২৪

১. একটি সরলরেখার সমীকরণ নির্ণয় করো যার ঢাল -2 এবং রেখাটি (4, -5) বিন্দু দিয়ে অতিক্রম করে।

সমাধানঃ

আমরা জানি,

m ঢালবিশিষ্ট (x₁ , y₁) বিন্দুগামী সরলরেখার সমীকরণ y - y₁ = m(x - x₁)

প্রদত্ত প্রশ্নে দেওয়া আছে,

m = - 2 ও (x₁,y₁) = (4,-5)

∵ y – (-5) = -2(x - 4) [মান বসিয়ে]

বা, y + 5 = -2x + 8

বা, y = -2x + 8 – 3

বা, y = -2x + 3 [ইহাই নির্ণেয় সমীকরণ]

২. A(3, -3) ও B(4, -2) বিন্দুগামী সরলরেখার সমীকরণ নির্ণয় করো। সরলরেখাটির ঢাল কত?

সমাধানঃ

আমরা জানি,

সরলরেখার ঢাল, m

y₁-y₂

= -------

    x₁-x₂

[এখানে, (x₁,y₁)=(3,-3); (x₂,y₂)=(4,-2)]

   -3-(-2)

= -------

     3-4

= ^-1/_-1

= 1

আবার,

m ঢালবিশিষ্ট (x₁ , y₁) বিন্দুগামী সরলরেখার সমীকরণ y - y₁ = m(x - x₁)

অর্থাৎ, y – (-3) = 1(x - 3)  [A(3, -3 বিন্দুর প্রেক্ষিতে]

বা, y + 3 = x – 3

বা, y = x – 3 – 3

বা, y = x – 6

∵ A(3, -3) ও B(4, -2) বিন্দুগামী সরলরেখার সমীকরণ: y = x – 6 এবং ঢাল m = 1.

৩. দেখাও যে, A(0, -3), B(4, -2) এবং C(16, 1) বিন্দু তিনটি সমরেখ। [এটা হলো অবস্থান মানচিত্রে স্থানাঙ্ক জ্যামিতি এর ৩ নং প্রশ্ন, নিচে বিস্তারিত দেয়া আছে।]

সমাধানঃ

আমরা জানি,

m ঢালবিশিষ্ট (x₁,y₁) ও (x₂,y₂) বিন্দুগামী সরলরেখার সমীকরণঃ y₁-y₂=m(x₁-x₂).

∵ m ঢালবিশিষ্ট A(0, -3) ও B(4, -2) বিন্দুগামী সরলরেখার সমীকরণঃ -3-(-2)=m(0-4)

বা, -3+2 = -4m

বা, -1 = -4m

বা, m = ¼

আবার,

m ঢালবিশিষ্ট B(4, -2) এবং C(16, 1) বিন্দুগামী সরলরেখার সমীকরণঃ -2-1=m(4-16)

বা, -3 = m(-12)

বা, m = ^-3/_-12

বা, m = ¼

অর্থাৎ, A(0, -3) ও B(4, -2) বিন্দুগামী সলরেখার ঢাল এবং B(4, -2) ও C(16, 1) বিন্দুগামী সলরেখার ঢাল একই।

∵ A(0, -3), B(4, -2) এবং C(16, 1) বিন্দু তিনটি সমরেখ [দেখানো হলো]।

৪. A(1, -1), B(t, 2) এবং C(t² , t + 3) বিন্দু তিনটি সমরেখ হলে t এর সম্ভাব্য মান নির্ণয় করো।

সমাধানঃ

m ঢালবিশিষ্ট (x₁,y₁) ও (x₂,y₂) বিন্দুগামী সরলরেখার সমীকরণঃ

y₁-y₂=m(x₁-x₂).

∵ m ঢালবিশিষ্ট A(1, -1) ও B(t, 2) বিন্দুগামী সরলরেখার সমীকরণঃ -1-2=m(1-t)

বা, -3= m(1-t)

বা, m = ^-3/_(1-t) ……….(i)

আবার,

m ঢালবিশিষ্ট B(t,2) এবং C(t², t+3) বিন্দুগামী সরলরেখার সমীকরণঃ 2-(t+3)= m(t-t²)

বা, 2-t-3 = m(t-t²)

বা, -t-1 = m(t-t²)

বা, m = (-t-1)/(t-t²) ……….(ii)

এখন, প্রদত্ত বিন্দু তিনটি সমরেখ; অতএব প্রত্যেক জোড় বিন্দুর সরলরেখার ঢাল এর মান সমান হবে।

∵ (i) ও (ii) হতে পাই,

-3/(1-t) = (-t-1)/(t-t²)

বা,-3(t-t²) = (1-t)(-t-1)

বা, -3t+3t² = -(1-t)(1+t)

বা, -3t+3t² = -(1-t²)

বা, -3t+3t² = -1+t²

বা, -3t+3t² +1-t² = 0

বা, 2t²-3t+1 = 0

বা, 2t²-2t-t+1 = 0

বা, 2t(t-1)-1(t-1) = 0

বা, (2t-1)(t-1) = 0

বা, 2t-1 = 0 অথবা, t-1 = 0

বা, 2t = 1   বা, t = 1

বা, t = ½         

∵ t = (1, ½)

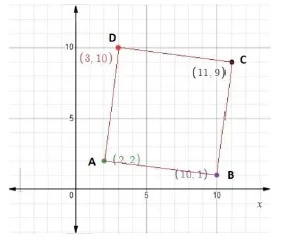
৫. A(2, 2), B(10, 1), C(11, 9) এবং D(3, 10) এই বিন্দুগুলো লেখচিত্রে বসাও এবং AB, BC, CD, AD রেখাংশ আঁকো। এই রেখাগুলো দ্বারা কী ধরনের ক্ষেত্র তৈরি হয়েছে? তোমার উত্তরের সপক্ষে যুক্তি দাও।

সমাধানঃ

লেখচিত্রে x ও y অক্ষ বরাবর ক্ষুদ্রতম বর্গের বাহুর দৈর্ঘ্যকে 1 একক ধরে A(2,2), B(10, 1), C(11, 9) এবং D(3, 10) বিন্দুগুলো স্থাপন করি।  এবং AB, BC, CD, AD রেখাংশ আঁকি।

এই রেখাগুলো দ্বারা একটি বর্গক্ষেত্র তৈরি হয়েছে।

যুক্তিঃ দুইটি বিন্দুর স্থানাংকের ভিত্তিতে,

AB = √{(10-2)²+(1-2)²}

= √{(8)²+(-1)²}

= √(64+1)

= √65

BC = √{(11-10)²+(9-1)²}

= √{(1)²+(8)²}

= √(1+64)

= √65

CD = √{(3-11)²+(10-9)²}

= √{(-8)²+(1)²}

= √(64+1)

= √65

AD = √{(2-3)²+(2-10)²}

= √{(-1)²+(-8)²}

= √(1+64)

= √65

অর্থাৎ, AB = BC = CD = AD

একইভাবে,

AC = √{(11-2)²+(9-2)²}

= √{(9)²+(7)²}

= √(81+49)

= √130

BD = √{(3-10)²+(10-1)²}

= √{(-7)²+(9)²}

= √(49+81)

= √130

অর্থাৎ, ABCD এর কর্ণদ্বয় (AC ও BD) পরস্পর সমান।

∵ AB, BC, CD, AD রেখাগুলো দ্বারা একটি বর্গক্ষেত্র তৈরি হয়েছে।

৬. তিনটি বিন্দুর স্থানাঙ্ক A(-2, 1), B(10, 6) এবং C(a, -6). যদি AB = BC হয়, তবে a এর সম্ভাব্য মানসমূহ নির্ণয় করো। a এর প্রতিটি মানের জন্য গঠিত ABC ত্রিভুজের ক্ষেত্রফল নির্ণয় করো।

সমাধানঃ

দেওয়া আছে,

তিনটি বিন্দুর স্থানাঙ্ক A(-2, 1), B(10, 6) এবং C(a, -6).

দুইটি বিন্দুর স্থানাংকের ভিত্তিতে পাই,

AB = √{(10+2)²+(6-1)²}

= √{(12)²+(5)²}

= √(144+25)

= √169

= 13

এবং,

BC = √{(a-10)²+(-6-6)²}

= √{(a-10)²+(-12)²}

=√{(a-10)²+144}

প্রশ্ন অনুসারে,

AB = BC

বা, 13 = √{(a-10)²+144}

বা, 169 = (a-10)²+144 [উভয়পক্ষকে বর্গ করে]

বা, (a-10)² = 169-144

বা, (a-10)² = 25

বা, a²-20a+10²-25=0

বা, a²-20a+100-25=0

বা, a²-15a-5a+75=0

বা, a(a-15)-5(a-15)=0

বা, (a-5)(a-15)=0

বা, a-5 = 0  অথবা, a-15=0

বা, a=5         বা, a = 15

∵ a= (5,15)

এখন,

a=5 হলে, তিনটি বিন্দুর স্থানাঙ্ক A(-2, 1), B(10, 6) এবং C(5, -6);

∵ ΔABC এর ক্ষেত্রফল

= ½[x₁(y₂-y₃)+x₂(y₃-y₁)+x₃(y₁-y₂)] [সূত্রানুসারে]

= ½[-2(6+6)+10(-6-1)+5(1-6)]

= ½[-2×12+10(-7)+5(-5)]

= ½[-24-70-25]

= ½×(-119)

= -59.5

কিন্তু ক্ষেত্রফল ঋণাত্মক হয় না।

∵ a=5 হলে, ΔABC এর ক্ষেত্রফল 59.5 বর্গ একক।

আবার,

a=15 হলে, তিনটি বিন্দুর স্থানাঙ্ক A(-2, 1), B(10, 6) এবং C(15, -6);

∵ ΔABC এর ক্ষেত্রফল

= ½[x₁(y₂-y₃)+x₂(y₃-y₁)+x₃(y₁-y₂)] [সূত্রানুসারে]

= ½[-2(6+6)+10(-6-1)+15(1-6)]

= ½[-2×12+10(-7)+15(-5)]

= ½[-24-70-75]

= ½×(-169)

= -84.5

কিন্তু ক্ষেত্রফল ঋণাত্মক হয় না।

∵ a=15 হলে, ΔABC এর ক্ষেত্রফল 84.5 বর্গ একক।

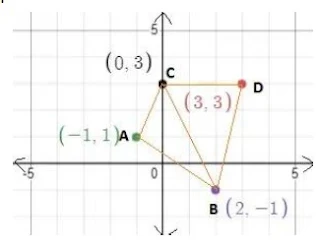
৭. চারটি বিন্দুর স্থানাঙ্ক A(-1, 1), B(2, -1), C(0, 3) ও D(3, 3)। বিন্দুগুলো দ্বারা গঠিত চতুর্ভুজের ক্ষেত্রফল নির্ণয় করো।

সমাধানঃ

দেওয়া আছে,

চারটি বিন্দুর স্থানাঙ্ক A(-1, 1), B(2, -1), C(0, 3) ও D(3, 3)। বিন্দুগুলোকে গ্রাফ কাগজে বসালে নিন্মোক্ত চতুর্ভুজ ABDC পাই।

∵ ΔABC এর ক্ষেত্রফল

= ½[x₁(y₂-y₃)+x₂(y₃-y₁)+x₃(y₁-y₂)] [সূত্রানুসারে]

= ½[-1(-1-3)+2(3-1)+0(1+1)]

= ½[-1×(-4)+2(2)+0(2)]

= ½[4+4+0]

= ½×(8)

= 4 বর্গ একক।

 এবং,

ΔBDC এর ক্ষেত্রফল

= ½[x₁(y₂-y₃)+x₂(y₃-y₁)+x₃(y₁-y₂)] [সূত্রানুসারে]

= ½[2(3-3)+3(3+1)+0(-1-3)]

= ½[2×0+3(4)+0(-4)]

= ½[0+12+0]

= ½×(12)

= 6 বর্গ একক।

∵ বিন্দুগুলো দ্বারা গঠিত চতুর্ভুজের ক্ষেত্রফল

= ΔABC এর ক্ষেত্রফল + ΔBDC এর ক্ষেত্রফল

= (4+6) বর্গ একক

= 10 বর্গ একক।

আরও দেখুন-

৮ম(অষ্টম) শ্রেণীর গণিত সকল অধ্যায়ের সমাধান pdf ২০২৪

 

Tag: ৮ম শ্রেণির গণিত বই সমাধান অধ্যায়-৬ অবস্থান মানচিত্রে স্থানাংকে জ্যামিতি , ৮ম শ্রেণির গণিত সমাধান অধ্যায়-৬ অবস্থান মানচিত্রে স্থানাংকে জ্যামিতি, ৮ম শ্রেণির গণিত অবস্থান মানচিত্রে স্থানাংকে জ্যামিতি সমাধান, ৮ম শ্রেণির গণিত সমাধান ২০২৪, ৮ম শ্রেণির গণিত সমাধান ২০২৪, ৮ম শ্রেণির গণিত সমাধান pdf, ৮ম শ্রেণির গণিত বই এর সমাধান, ৮ম শ্রেণীর গণিত বই pdf ২০২৪, class 8 math solution pdf, class 8 math solution 2nd chapter pdf , class eight math solution pdf 2024